承接Binary, 拥抱ternary和one-hot-neurons
之前有个blog是转载R2RT的BSN网络。后续他又发了一篇关于BSN的进阶,不过没有做深度优化。在这里我再把他用中文转载出来说一下。如果对原贴感兴趣可以查看这里. 如果对我注释的代码感兴趣,或者对里面各种矩阵的形状感兴趣可以看这里.
N-ary neurons
Binary神经元只能输出0或者1。万一我们希望有更多选择,像是不同颜色,渐变起来我们希望给他赋予整数值好区分。[0,1,2,3…]或许是个好的选择。在这里我们考虑一下简单的case。也就是当我们只有3种颜色的时候,我们可以定义他们为[-1,0,1]。我们希望有这样一个激活函数,像是梯子一样经过这3个区间。为什么呢?因为如果不是梯子,不是扁平的,如果是倾斜的像斜率为1的曲线的话那么当这个神经元在学习的时候就不会好好待在那个地方,而是被迫往其他地方转移。
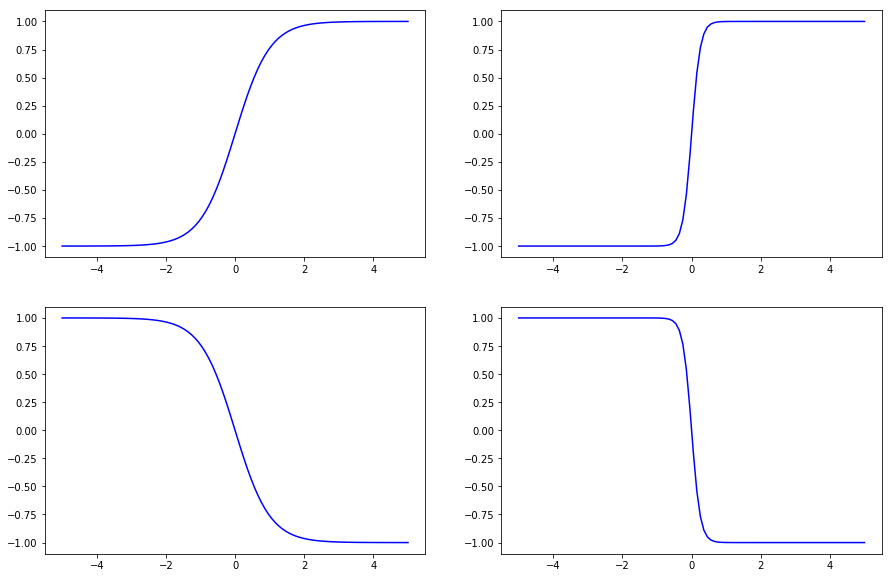
简单来说我们希望有一个这样的函数:
import matplotlib.pyplot as plt
import numpy as np
def f(a,x):
return np.tanh(a*x)
x = np.linspace(-5,5,100)
plt.figure(figsize=(15,10))
plt.subplot(221)
plt.plot(x,f(1,x),'b')
plt.subplot(222)
plt.plot(x,f(4,x),'b')
plt.subplot(223)
plt.plot(x,f(-1,x),'b')
plt.subplot(224)
plt.plot(x,f(-4,x),'b')
plt.show()
def f_acti(x,a=1.5,b=0.5):
return a*np.tanh(x) + b*np.tanh(-3*x)
plt.figure(figsize=(15,7))
plt.plot(x, f_acti(x,a=1.5,b=0.5),'-', linewidth=1.5)
plt.grid(True)
plt.xticks(np.linspace(-5,5,20))
plt.show()
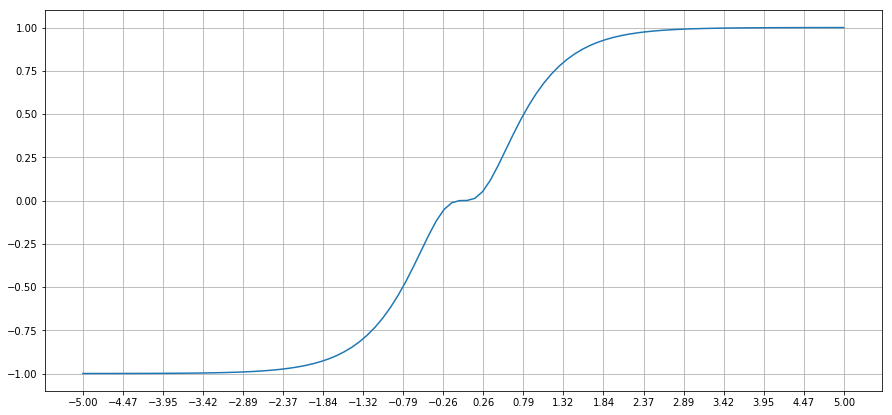
可以看到这个函数不像$\tanh$, 它还会在0处短暂停留。因此它可以输出多一个维度。
One-hot neurons
另外一种情况,当你的输出不具有线性,选择ternary或者n-ary就不是一个较好的选择。当然这个只是我的臆想,具体实验似乎没有证明这点。比如说地名,比如[Boston, New York, Toronto, Houston]这个组里面就不具备线性的相关性。怎么办呢,我们可以考虑数据One-hot neurons。所谓One-hot, 即给定的维度里只有一个1,其余都是0。这意味着假设你有个20个features,我想简化一下它的表现形式,只突出重点来,可以把20个features分成5组4维的数组,但是每个小的数组里只有一个1.比如说:
features = [[0,0,0,1],
[0,0,1,0],
[0,0,1,0],
[0,1,0,0],
[1,0,0,0]]
当然一开始features并不长这样,都可能是一些连续的数字带有小数点。那么如何长这样呢,就是通过随机抽样或者取最大值的序号再转化为one-hot向量。
BP的过程
这里面的BP跟BSN一样,都需要自定义的。Tensorflow有关于如何自定义BP的一些指点,不过不是很全。详情看stackoverflow吧。举个例子:
def st_sampled_softmax(logits):
"""Takes logits and samples a one-hot vector according to them, using the straight
through estimator on the backward pass."""
with ops.name_scope("STSampledSoftmax") as name:
probs = tf.nn.softmax(logits)
onehot_dims = logits.get_shape().as_list()[1]
res = tf.one_hot(tf.squeeze(tf.multinomial(logits, 1), 1), onehot_dims, 1.0, 0.0)
with tf.get_default_graph().gradient_override_map({'Ceil': 'Identity', 'Mul': 'STMul'}):
return tf.ceil(res*probs)
def st_hardmax_softmax(logits):
"""Takes logits and creates a one-hot vector with a 1 in the position of the maximum
logit, using the straight through estimator on the backward pass."""
with ops.name_scope("STHardmaxSoftmax") as name:
probs = tf.nn.softmax(logits)
onehot_dims = logits.get_shape().as_list()[1]
res = tf.one_hot(tf.argmax(probs, 1), onehot_dims, 1.0, 0.0)
with tf.get_default_graph().gradient_override_map({'Ceil': 'Identity', 'Mul': 'STMul'}):
return tf.ceil(res*probs)
@ops.RegisterGradient("STMul")
def st_mul(op, grad):
"""Straight-through replacement for Mul gradient (does not support broadcasting)."""
return [grad, grad]
结论
从实验上来看,ternary表现似乎没有binary好,这也可能是作者并没有完全优化与实现slope-annealing的原因。还有可能是因为MNIST本身不够复杂,ternary可能更适合用在大型,更多维度的数据集上。